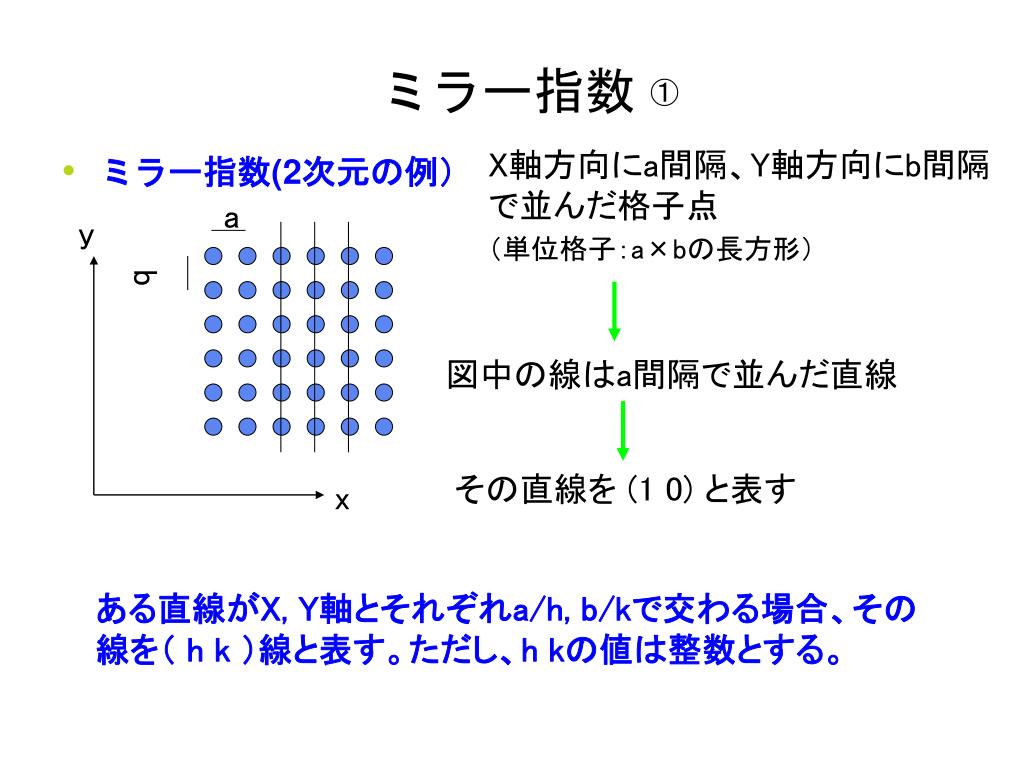
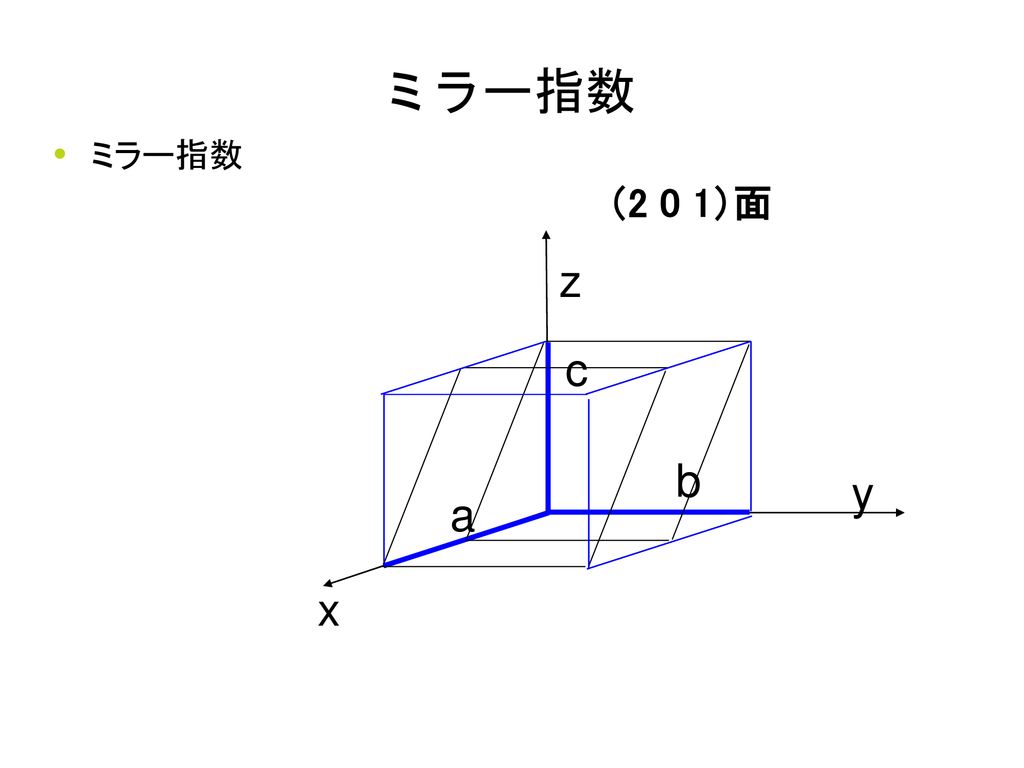
ミラー指数(面) 3 手順5 ミラー指数は整数を使う約束ですから,分母の最小公倍数を掛けて同じ比の最小の整数比に直します. いまの場合6,3,2 になります.この面のミラー指数は(632) と表記し,「ろく・さん・に・めん」と読み ます. 交点がマイナス方向で座標軸を切ったときは指数の上に六方 6 6 6/m 622 6mm 6m2 6/mmm 三方 3 3 32 3m 3m 正方 4 4 4/m 422 4mm 4m2 4/mmm 斜方 222 mm2 mmm 単斜 2 m 2/m 三斜 1 1 晶系 N N NmN 2 N m N m N mm 赤色で示した結晶点群– ラウエ群(Laue cleass)、対称心をもつ 回折(X線、中性子、電子)パターンに現れる点群 単位胞の選び方-規則1 規則1 -結晶系の決め方 立方晶系 · 六方晶 ミラー指数 について 今六方晶のミラー指数が 001 100 101 102 110 と表されております。 ここで、この3桁のミラー指数を全て4桁で表すとどのようになりますか? よろしくお願いし
結晶とは コトバンク
六方晶 ミラー指数 3指数
六方晶 ミラー指数 3指数-ミラー指数 結晶面の指数 括弧の定義 六方晶の場合 Title PowerPoint プレゼンテーション Author Yoichi Nabetani Last modified by nabetani Created Date 12/28/04 AM Document presentation format 画面に合わせる (43) Company University of Yamanashi Other titles Times New Roman MS Pゴシック Arial Calibri Symbol 標準デザイン Microsoft · 六方晶 ミラー指数 について 今六方晶のミラー指数が 001 100 101 102 110 と表されております。 ここで、この3桁のミラー指数を全て4桁で表すとどのようになりますか? よろしくお願いし



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download
六方晶の場合のミラー指数のことを六方晶指数と言うことがある。 (ja) ミラー指数(ミラーしすう)は結晶の格子中における結晶面や方向を記述するための指数である。英国の鉱物学者ウィリアム・ハロウズ・ミラー (William Hallowes Miller) によって考案された。 ミラー指数には、面指数と方向指数(方位指数)の2種類がある。面指数は結晶や格子をどのような平面で切るか機能材料組織学 第 7 回 前回: ・すべり系 ・ミラー指数 ・ミラー指数の一括表示 今回: ・ミラー・ブラベー指数 ・分解せん断応力 ・単結晶の降伏応力 「機能材料組織学」第 7 回 71 ミラー・ブラベー指数 ・六方晶の場合: 図 71 六方晶の単位格子 方向の表示法 図 72 ミラー・ブラベー指数の表示法(方向) 別解: 図 73 ミラー・ブラベー指数の表示法 (方向3回 ミラー指数の決め方を理解し、結晶の概形にミラー指数をつける。 (プリント、pp3134、演習21) 7結晶系(立方、正方、斜方、単斜、三斜、三方、六方)の名称を覚える。 4回 ステレオ投影図の作成法を理解し、斜方晶系と正方晶系を描く。
ミラー指数(hkl) ☆六方晶(hexagonal)の場合 六方晶の単位格子(単純単位格子) はa=b6=c で、α = β = π/2、γ = 2π/3 となるも のである。正規直交座標の軸はそれぞれx 軸、y 軸、z 軸であるが、結晶のa 軸とx 軸を 一致させ、さらにc軸とz 軸がそれぞれ一致するように座標軸を重ねることができる。こ 3解法(a) (・3)式に格子定数とミラー指数を代入する. (b) {399}面のミラー指数は{133}面の3倍である.したがって 面間隔は1/3である. 答.0063nm 0190nm 2767 075 3 094 3 0 1 1 2 2 2 2 2 2 2 2 = ∴ = = = d d d 答.019nm · 六方晶の4指数記法 (と3指数記法との対応関係) この記事では,六方晶系の面指数・方位指数における4指数3指数の対応関係について備忘録として簡単にお話しさせていただきます. 六方晶は6回回転対称軸または6回回反対称軸を持っている結晶系であり,a1
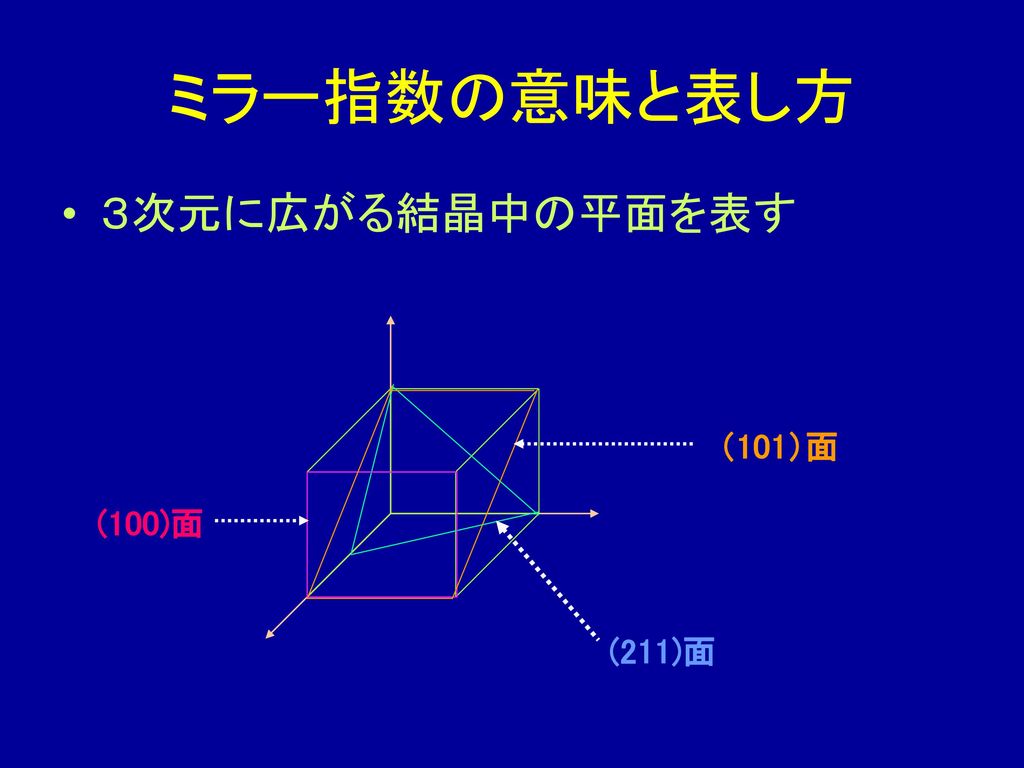
格子定数 求め方 立方晶 (i) 単位格子一辺の長さ l と原子半径 r の関係 結晶の単位格子の形と大きさを表すパラメーターを「格子定数 (lattice constant) 」といいます。 一般的には、単位格子の各綾の長さ (3 つの結晶軸の各方向にそった繰り返しの周期) の a, b指数(ミラー(Miller) 指数)と呼ぶ。図の例では、A = 3, B = 2, C = 2 であるので、 1 3 2 2 であり、従ってミラー指 数は(2 3 3) となる。指数の0 は切片が無限大であること、つ まり切片を持たないことを意味する。 (100) (010) (011) (111) 図4 格子面(ミラー指数)の例ミラー指数(ミラーしすう)は結晶の格子中における結晶面や方向を記述するための指数である 。 英国の鉱物学者ウィリアム・ハロウズ・ミラー (William Hallowes Miller) によって考案された。 ミラー指数には,面指数と方向指数(方位指数)の2種類がある。面指数は結晶や格子をどのような平面で




Woa1 リチウムイオン二次電池用正極活物質及びリチウムイオン二次電池 Google Patents




13 号 誘電体磁器組成物および電子部品 Astamuse
六方晶系の面指数 を用いる (h k l) # (h k j l) A B D O OAB = OAD OBD h k j = 0 利点:面の対称性が明らかになる この2つの面が等価であることがわかる六方晶の (110)面と等価な面を、ミラー・ブラベー指数 (hkil)で表記せよ� 4つの整数の組のミラー指数 (三方晶・六方晶) 三方晶や六方晶は、ある軸を中心として1° 回転させると同一の結晶構造となる。六方晶におけるミラー指数 六方晶における主要な面 底面 錐面 柱面




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



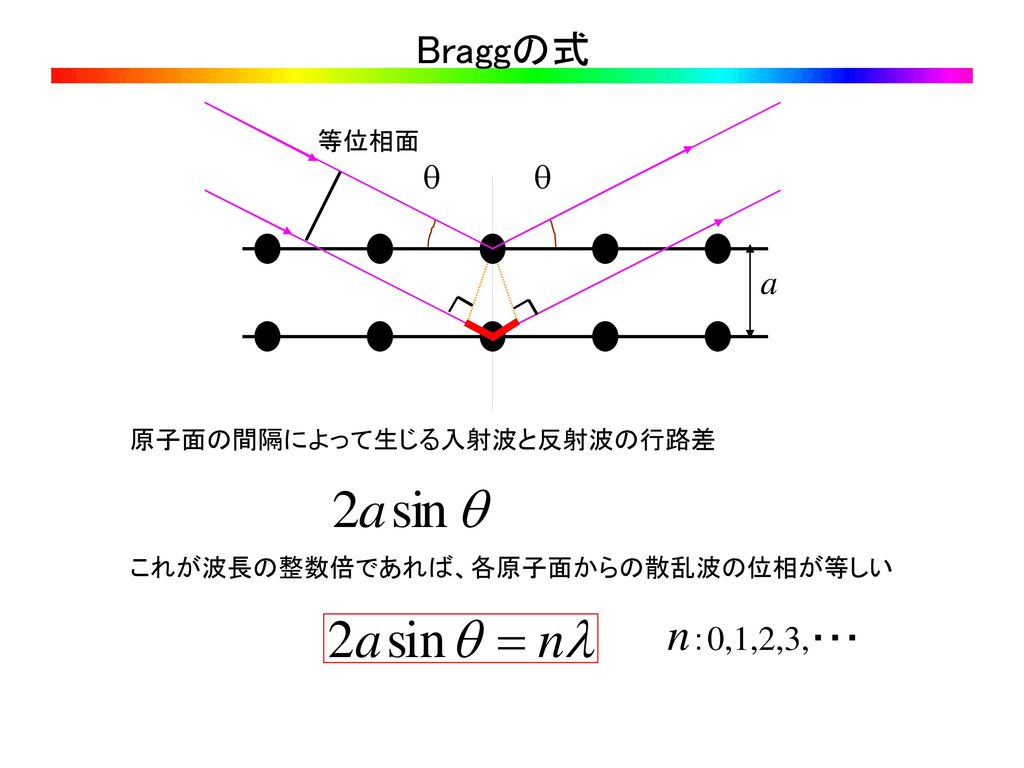
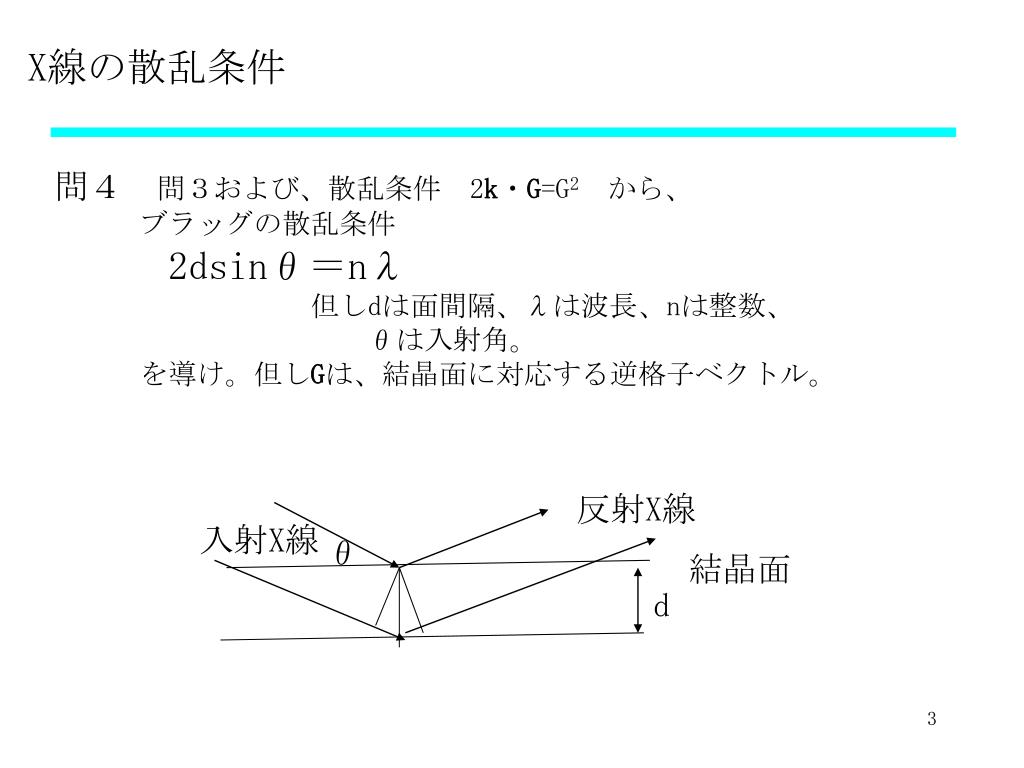
x線結晶解析におけるラウエの条件式とブラッグの条件式
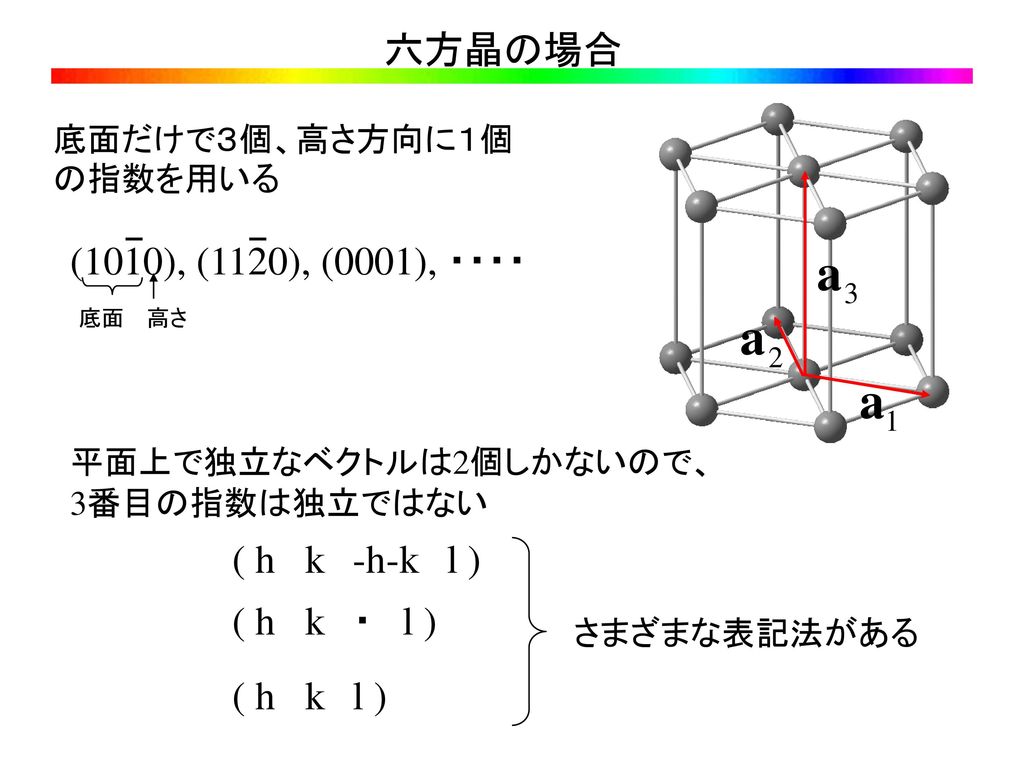
7ミラー指数 8逆格子 9回折条件 結晶構造解析i 結晶構造解析ii 結晶欠陥(転位,空孔,格子間挿入,置換) 結晶成長 立方格子 面心格子,六方格子 ブリルアンゾーン 空間群 光学モードと音響モード フォノン=場の量子化もどき ボゴリューボフ変換 2次元格子 · 図2 主なミラー指数の方向表示例 ここで、体心立方格子、面心立方格子、稠密六方格子の代表的なすべり面とすべり方向を図3に示します。稠密六方格子は立方体から六角形になるので表示方法が複雑になるので詳細は割愛しますが、4桁の表示になります六方晶の場合 a 1 a 2 a 3 底面だけで3個、高さ方向に1個 の指数を用いる (1010), (11), (0001), ・・・・ 底面 高さ 平面上で独立なベクトルは2個しかないので、 3番目の指数は独立ではない ( hkhkl ) ( hk・l ) ( hkl ) さまざまな表記法がある



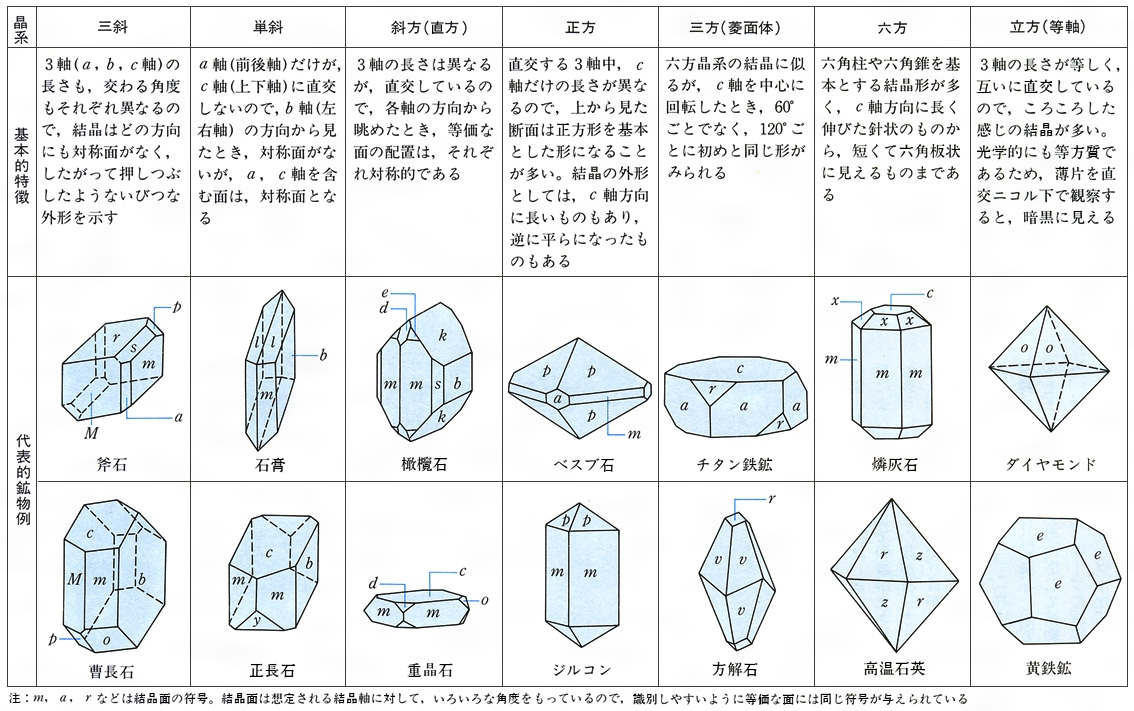
鉱物の結晶




結晶とは コトバンク
· a 3 → {\displaystyle {\vec { {a}_ {3}}}} を取ったとする。 このとき、格子点同士を結ぶ任意のベクトル A → {\displaystyle {\vec {A}}} は、整数の組K, L, M を用いて A → = K a 1 → L a 2 → M a 3 → {\displaystyle {\vec {A}}=K {\vec { {a}_ {1}}}L {\vec { {a}_ {2}}}M {\vec { {a}_ {3}}}} の形で書き表される。 この事実により結晶学では『方向 A → {\displaystyle {\vec {A}}}ミラー指数(ミラーしすう)は結晶の格子中における結晶面や方向を記述するための指数である 。英国の鉱物学者ウィリアム・ハロウズ・ミラー (William Hallowes Miller) によって考案された。 ミラー指数には、面指数と方向指数(方位指数)の2種類がある。面指数は結晶や格子をどのような平面で切るかを指定し、方向指数は結晶、格子内での方向を指定する。3 は有理数なので、適当な整数 m を掛けて、 h 1=mh' 1, h 2=mh' 2, h 3=mh' 3 が最小の整数の組となるようにする (h 1, h 2, h 3は整数で互いに素の組 ) は原点に最も近い格子面 に対応 ミラー指数に対応する格子面は原点に最も近い格子 面 元のABC の面は原点から m 番目の格子面



無機化合物の構造と特性 との関係を理解する Ppt Download




13 号 sicエピタキシャルウエハおよびそれを用いたsic半導体素子 Astamuse
(a =b ≠ c, α=β=π/2, γ= 2π/3) (a =b = c, α=β=γ≠π/2) 六方晶系(hexagonal system) 三方晶系(trigonal system) 体心立方格子 面心立方格子 最密六方格子 (a =b ≠ c, α=β=γ=π/2) 正方晶系(tetragonal system) 立方晶系(cubic system) ブラベー格子 基本単位格子 12ミラー指数 ミラー指数の表記 < 100>=100,010,001 { 111}=(111),(1 11),(11 1),(111) 方向: 面: 5 立方晶における主要な面 立方晶における重要な関係 ( hkl)!hkl dhkl= a h2k2l2 a:格子定数 面間隔 6 六方晶におけるミラー指数 結晶格子の面間隔を計算する方法について、紹介します。今回は六方晶に2.ブラベー・ミラー指数 六方結晶族に属する結晶は六方単位胞でも菱形単位 胞でも記述できる.ブラベー格子は菱形の場合,六方単 位胞は慣用単位胞であるがその多重度(単位胞内の格子 点の数)は3である.一方,菱形単位胞は単純単位胞だ が慣用ではない(基底の軸は格子の対称方向と



Space Group For Crystal Structure Analysis




逆 格子 ベクトル
また、六方晶系以外の場合(ほとんど全ての結晶)と六方晶の場合(例外的)で、ミラー指数のつけ方が少々異なる。 六方晶の場合のミラー指数のことを六方晶指数と言うことがある。 目次 1 六方晶系以外の場合 11 方向指数;六方晶系以外の場合 まず六方晶系以外の場合におけるミラー指数を方向指数、面指数の順に説明する 方向指数 二次元結晶の結晶軸とは本来、基本並進ベクトルと称される2本のベクトルであるべきだが、実際には回転対称性などを考慮し、基本並進ベクトルとは限らない(2本の)格子六方晶系の面指数 a b d a b c a b d c, , , , , o を用いる (h k l) → (h k j l) A B D a h a k O a j OAB = OAD OBD 1 1 1 sin1 sin60 sin60 2 2 2 a a a a a a h k h j j k q q q h k j = 0 利点:面の対称性が明らかになる (1 2 1) (1 1 1) (1 2 1 1) (1 1 2 1) この2つの面が等価であることがわかる




Wo13 号 窒化ガリウム系化合物半導体発光素子及びそれを用いた光源装置 Astamuse




14 5615号 立方晶炭化珪素半導体基板及び立方晶炭化珪素層 Astamuse
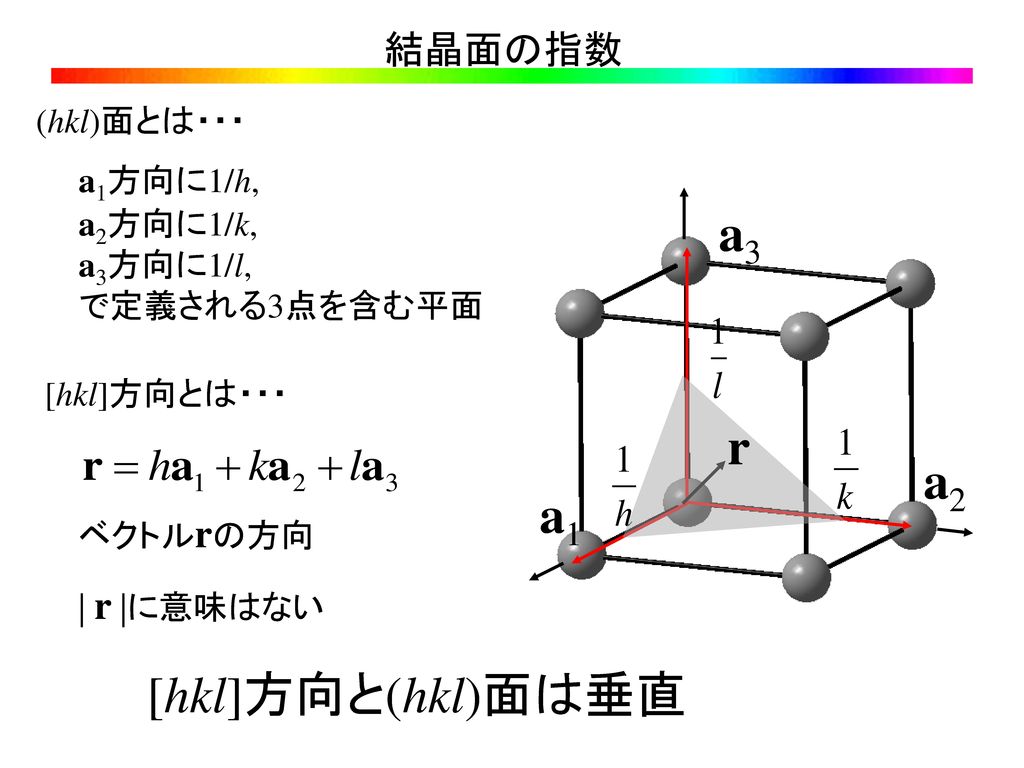
ミラー指数は というふうに,「丸括弧の中の3つの整数」で表示し, それによって任意の格子面を表現することができます. ここでは,任意の格子面をミラー指数で表現する手続きを紹介します. 面のミラー指数を得る手順 は 軸, は 軸, は 軸とそれぞれ対応しています. 手順 1 単位格子ミラー指数(ミラーしすう)は結晶の格子中における結晶面や方向を記述するための指数である 。 英国の鉱物学者ウィリアム・ハロウズ・ミラー (William Hallowes Miller) によって考案された。 ミラー指数には、面指数と方向指数(方位指数)の2種類がある。面指数は結晶や格子をどのような平面でを,正方晶用と六方晶用(三方晶兼用)にそれぞれ 枚の図表にまとめている 。 ˘ˇ に の正方晶用の図表を,筆者が文 献 を参考に作図した物を示した。横軸上段が, ミラー指数の とを下段がを示している。上下 それぞれの点を結ぶ曲線が,格子定数の比( )




Woa1 リチウムイオン二次電池用正極活物質及びリチウムイオン二次電池 Google Patents
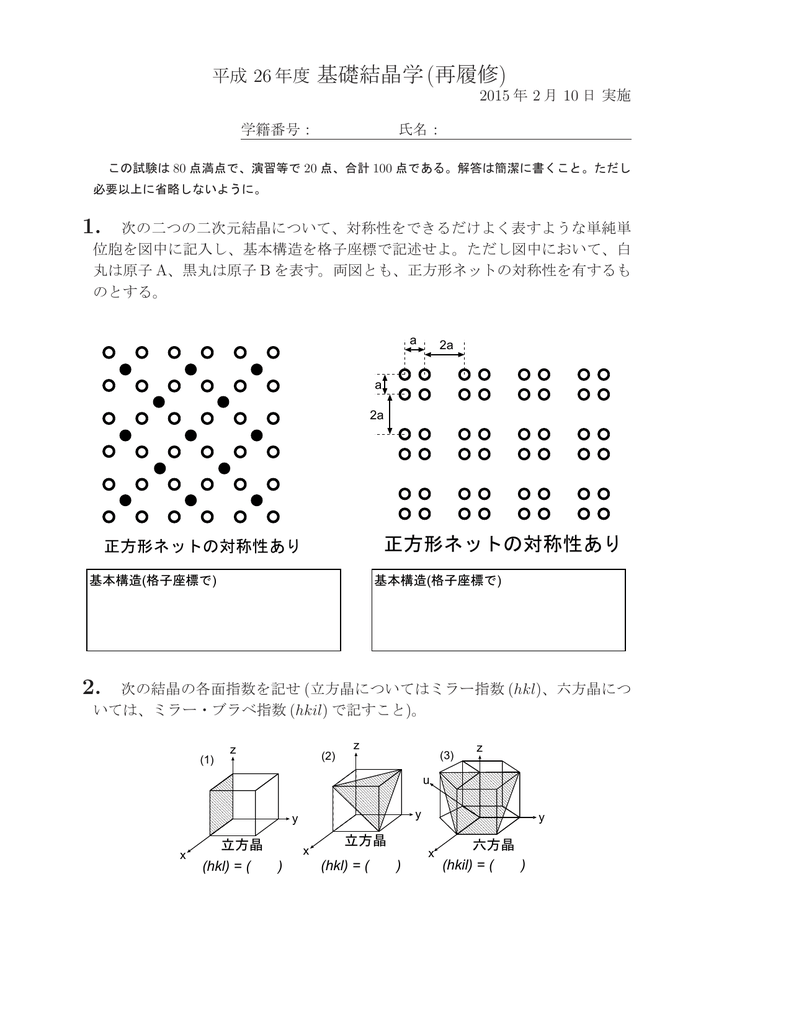



平成 26年度基礎結晶学 再履修
· ミラーブラベー指数 i 六方晶系結晶の方向、ベクトル法と垂直射影法2 10 ミラーブラベー指数 ii 六方晶系結晶の面の記述法2 11 結晶中の格子欠陥の種類 八面体および四面体位置と空隙3 12 材料試験法の概論 引張り試験と応力ひずみ線図を中心にして 4 13 金属のすべり変形 す六方晶におけるミラー指数 六方晶における主要な面 底面 錐面 柱面 8 六方晶における主要な方向 Polar Stereographic Polar Stereographic Equatorial Stereographic Oblique Stereographic ステレオ投影 9 ステレオ投影の原理 ステレオ 投影の原理 極点 の位置 10 極点の位置 極点の位置 11 (001) 標準ステレオ六方用指数(Hexagonal index)とも呼ばれる六方晶における結晶方向および結晶面方位を表すための指数のこと.結晶底面に平行で,それぞれが1°の方位差を有する格子ベクトル \({a_1}\), \({a_2}\), \({a_3}\)および,それらのベクトルと垂直な格子ベクトル \({c}\)を結晶軸として,指数を決定する



半導体物理 結晶構造について 2 Sciencompass




2 ミラー指数についてpart2 Youtube
ミラー指数について 構造説明文中の {1 0 0}やなどは、結晶面および結晶中の方向を示すミラー指数と呼ばれる指標です。 3つの整数 h, k, l を用いて ( h k l )、 { h k l } が結晶面を、 h k l 、< h k l > が結晶中の方向を表します。 各々の前者が単一の面と六方晶 六方晶においては慣用的に下図のような a 1 , a 2 , a 3 , c の四つの軸を用いて方向面を表し,指数を( hklm )と書きます。この方法では,Z軸方向の指数は0001となります。この4軸を用いると,a 1 , a 2 , a 3 方向を現す指数 hkl の間には, h k = l332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download




Woa1 非水電解質二次電池用正極活物質とその製造方法 および 非水電解質二次電池 Google Patents



Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



x線結晶解析におけるラウエの条件式とブラッグの条件式



逆 格子 ベクトル 実格子と逆格子の対応 物理のかぎしっぽ




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度
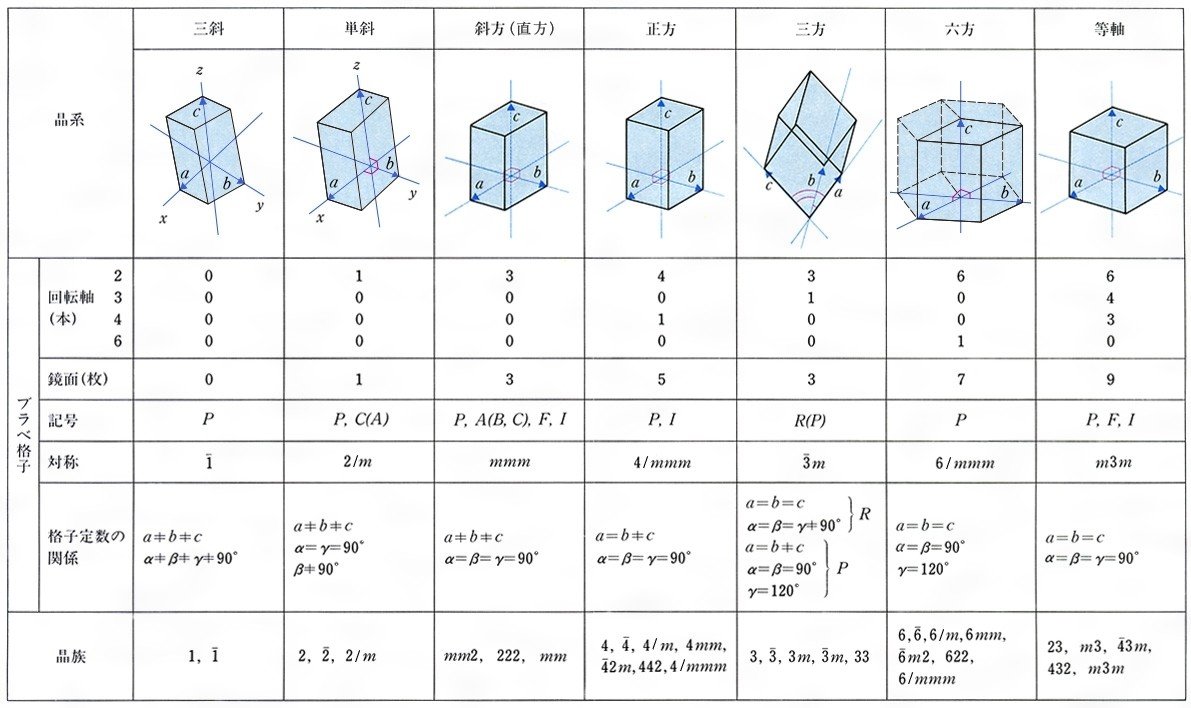



Images Of 晶系 Japaneseclass Jp




Wo10 号 窒化物系半導体素子およびその製造方法 Astamuse




ミラー指数 Wikiwand




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
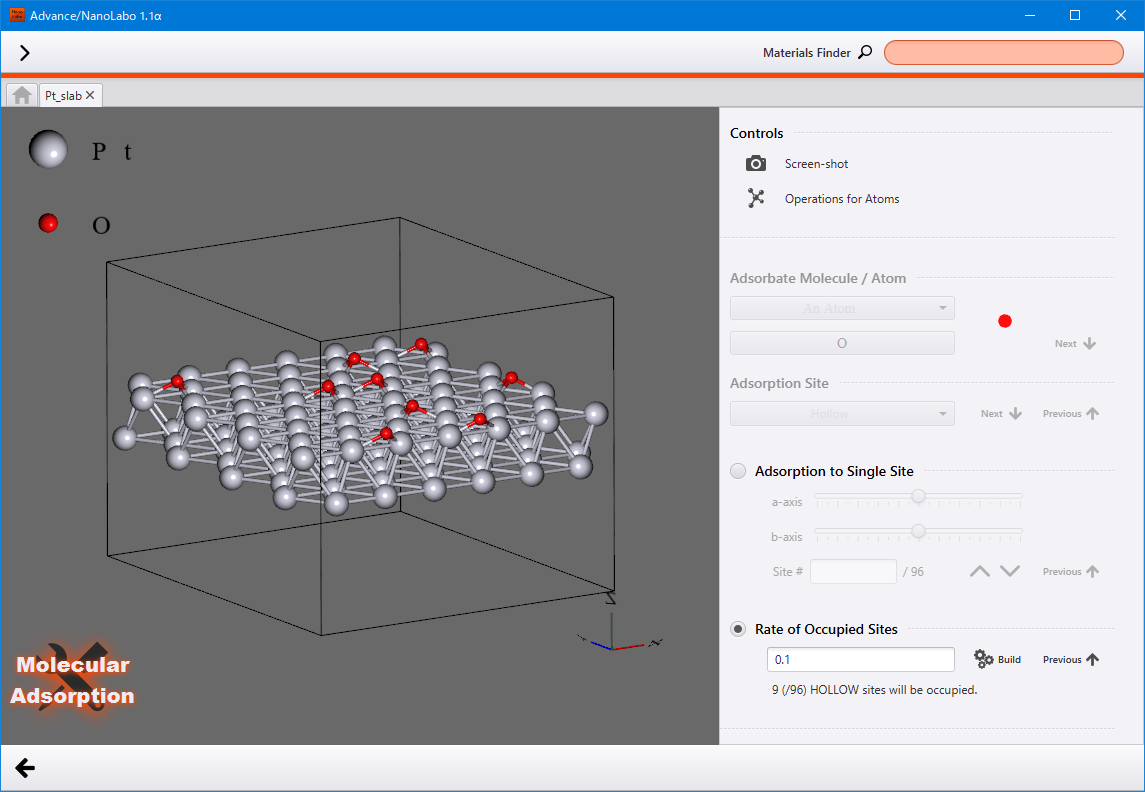



モデラ Advance Nanolabo ドキュメント




โน ตของ 専門 講義 結晶構造について ช น Clear



x線結晶解析におけるラウエの条件式とブラッグの条件式




ミラー指数 Monozukuri Hitozukuri 日本のものづくり




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download



Information




Wo14 号 半導体発光装置 Astamuse




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度




Woa1 化合物エピタキシャル層の製造方法 化合物エピタキシャル層 半導体積層構造および半導体発光デバイス Google Patents
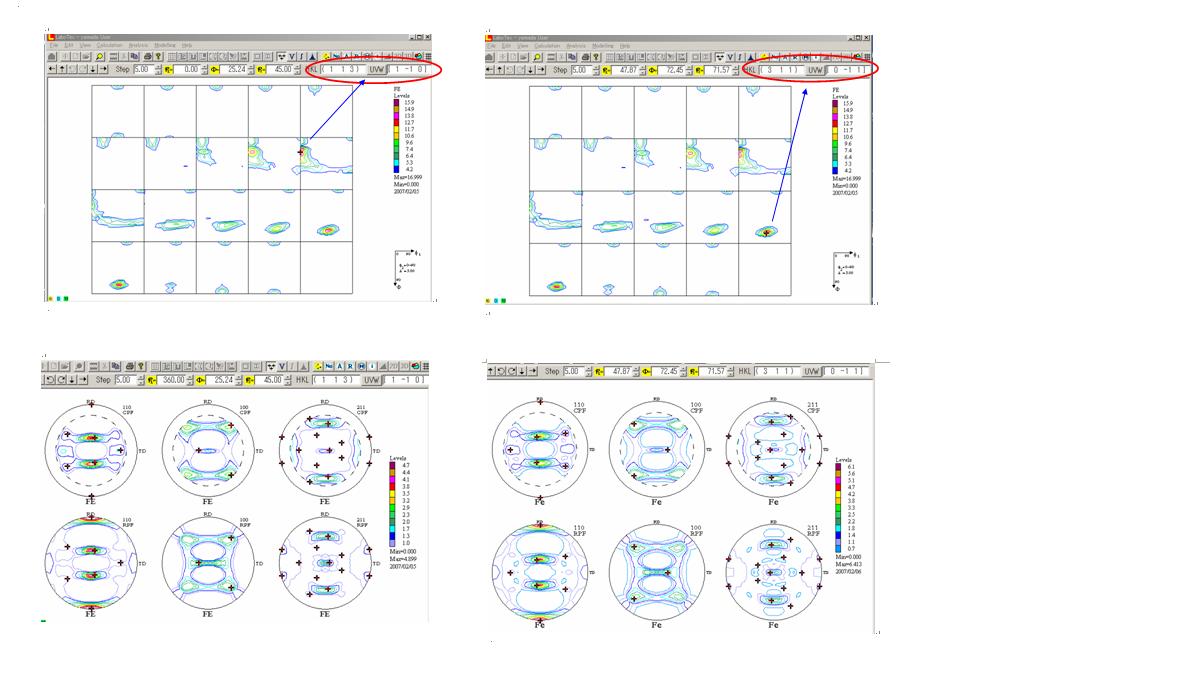



無理やりのfe試料による極点処理 立方晶odf解析シリーズ 方位決定 極点測定 解析 Odf Labotexの導入 helpertex




Wo11 号 窒化物系半導体素子およびその製造方法 Astamuse



Mukikotaikagaku




13 0631号 sicエピタキシャルウエハおよびそれを用いたsic半導体素子 Astamuse




2 2 1 ブラベー格子 単位格子 原子が配列している周期的な配列の中で最も 単純で最小な単位 Ppt Download
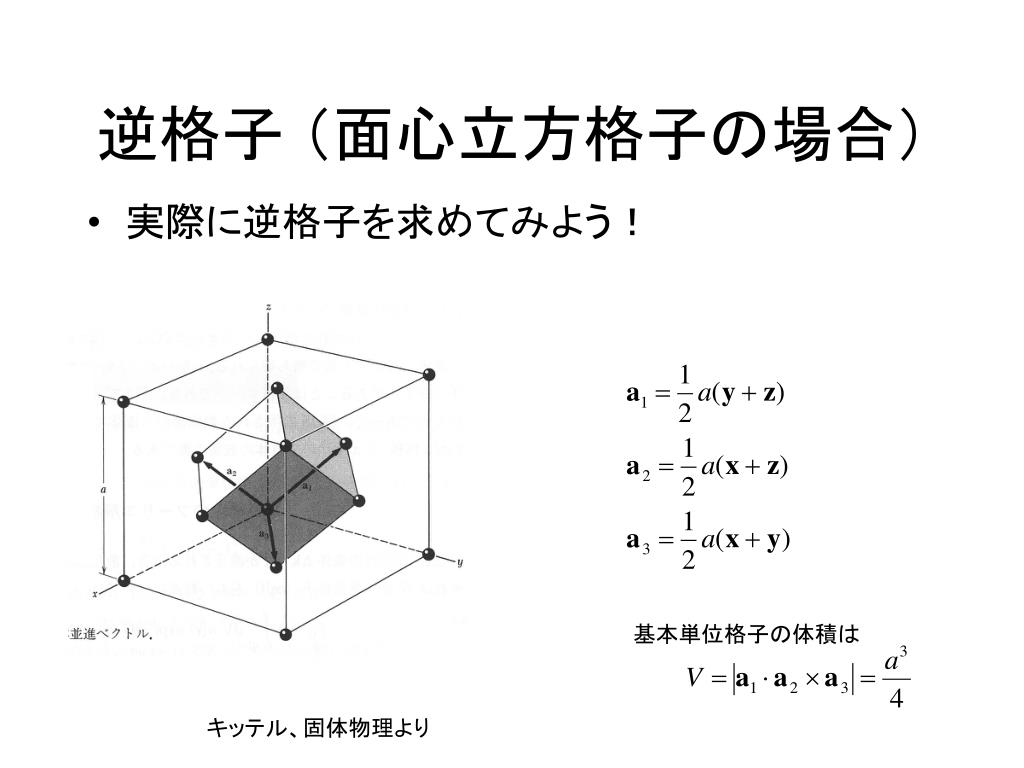



逆 格子 ベクトル 実格子と逆格子の対応 物理のかぎしっぽ




前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download




逆 格子 ベクトル




โน ตของ 専門 講義 結晶構造について ช น Clear




前回の内容 結晶工学特論 第3回目 格子歪 結晶の歪 歪 応力 歪エネルギーの定義 不整合歪 基板と成長層の格子不整合に起因する歪 Ppt Download
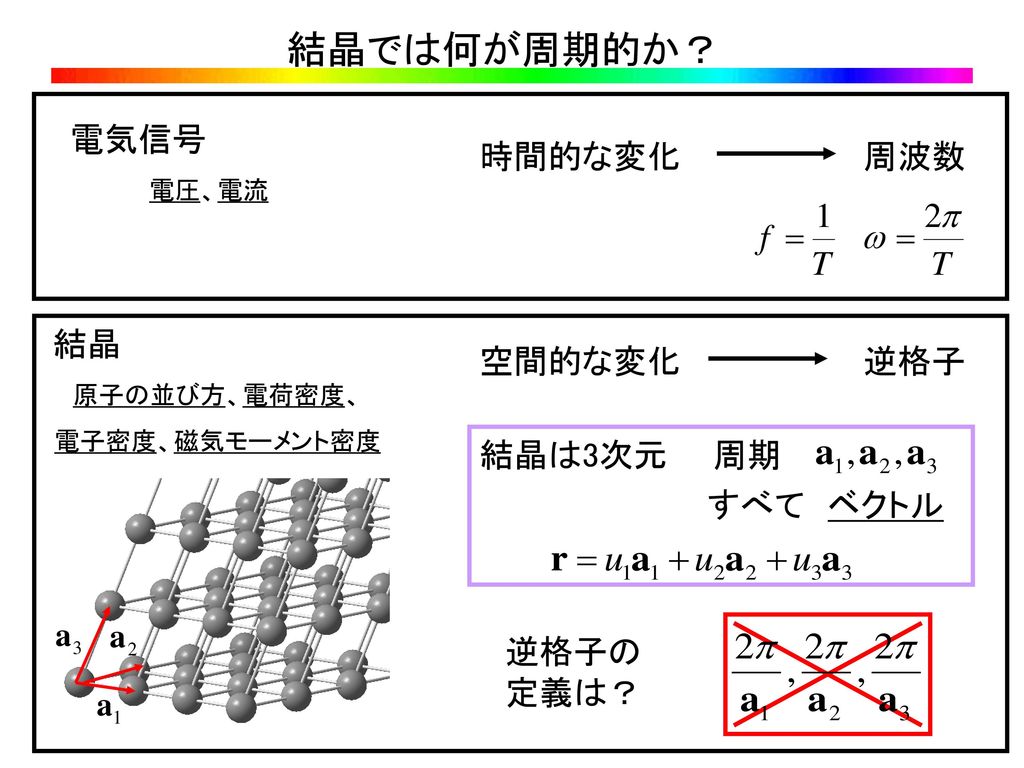



前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download



Space Group For Crystal Structure Analysis




Wo13 号 半導体発光素子 その製造方法及び光源装置 Astamuse




ミラー指数 Monozukuri Hitozukuri 日本のものづくり




Wo07 号 単結晶サファイア基板 Astamuse




ミラー指数 Monozukuri Hitozukuri 日本のものづくり




ミラー指数 Wikipedia




17 号 結晶方位の解析方法およびその解析装置 Astamuse



x線結晶解析におけるラウエの条件式とブラッグの条件式




Woa1 非水電解質二次電池用正極活物質とその製造方法 および 非水電解質二次電池 Google Patents



半導体物理 結晶構造 3 ミラー指数 Sciencompass




Mbaheblogjpnmry ミラー指数 方向 2710 ミラー指数 方向 角度



x線結晶解析におけるラウエの条件式とブラッグの条件式



0 件のコメント:
コメントを投稿